Spannungs-Dehnungs-Diagramm

Dabei wird ein genormter Metallstab langsam auseinandergezogen bis der Stab unter der Last nachgibt und bricht. Vom Anfang des Zugversuches bis zum Bruch verhält sich das zu testende Material unterschiedlich, was im Spannungs-Dehnungs-Diagramm dargestellt wird.

Außerdem kann die elastische Verformungsgrenze, die plastische Verformungsgrenze, die maximale Zugstärke und Bruchgrenze abgelesen werden. Diese Werte sind vor allem für Konstrukteure von größter Wichtigkeit, da so herausgefunden werden kann, wie viel Kraft ein Werkstoff, in Bezug auf den verwendeten Querschnitt, aufnehmen kann, ohne sich dauerhaft zu verformen.

Der Graph im Diagramm zeigt an, wie stark sich das Material unter der steigenden Spannung dehnt. Betrachtet man den Verlauf der Kurve genauer, so kann in den meisten Fällen das Verhalten des Werkstoffes in vier Phasen unterteilt werden.

Diese werden als:

elastische Verformung
plastische Verformung / Fließzone
plastische Verformung / Kaltverfestigung
plastische Verformung / Einschnürung

bezeichnet. Der Zugversuch endet mit dem Bruch des Metallstabes.

Dies bedeutet, dass das Material nur im Bereich der ersten Phase, der elastischen Verformung, ohne Deformationen oder Beschädigungen in den Ausgangszustand zurückkehrt, wenn die Zugkraft wieder verringert wird. In den folgenden Phasen ist die Verformung von Dauer und somit irreversibel.

Die Daten eines Spannungs-Dehnungs-Diagramms sind verlässlich. Jedoch sind die angegebenen Werte von einigen Variablen abhängig, die die Messergebnisse direkt beeinflussen. Dazu zählen die Art der Materialherstellung, die Werkstoffzusammensetzung, mikroskopische Unvollkommenheiten und die Temperatur. Aus diesem Grund ist das Diagramm eines jeden Zugversuches etwas anders und es sind immer mehrere Zugversuche nötig, um mit den ermittelten Durchschnittswerten ein verlässliches Spannungs-Dehnungs-Diagramm zu erstellen.

Die Interpretation

Um dieses Diagramm vollständig zu verstehen, ist die Kenntnis einiger Fachbegriffe von großer Wichtigkeit. Wie bereits beschrieben, gibt das Spannungs-Dehnungs-Diagramm die mechanischen Eigenschaften von Werkstoffen, wie zum Beispiel Stahl, Edelstahl oder Aluminium wieder.

Aus dem Diagramm kann abgelesen werden, um wie viel sich das Material im Verhältnis zu einer steigenden Krafteinwirkung strecken kann.

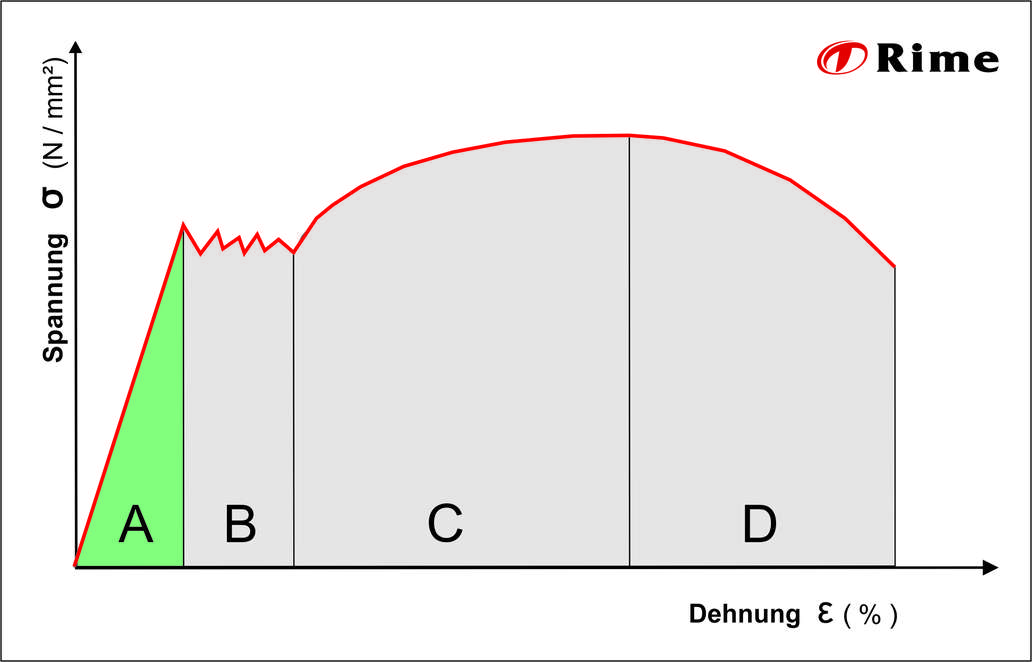
Im Diagramm gibt die horizontale Achse die Dehnung in Prozent an. Die Spannung wird auf der vertikalen Achse dargestellt. Der Graph wird in vier Bereiche (A-D) unterteilt, von denen der erste Abschnitt die elastische Verformung darstellt.

In den verbleibenden Bereichen findet dann nur noch die plastische Verformung statt. Jedoch verhält sich das Material in jeder einzelnen Phase der plastischen Verformung unterschiedlich. Bereich B definiert die Fließzone.

Das ist ein Bereich, in dem das Material über die elastische Belastbarkeit strapaziert wird und die ersten plastischen Verformungen auftreten. In der Fließzone wechselt mit steigender Dehnung die Spannung sehr unregelmäßig, sodass im Kurvenverlauf eine Wellenlinie entsteht. Im Abschnitt C steigt die Spannung weiter stark an, wobei auch die plastische Verformung zunimmt. Ist das Maximum der Belastbarkeit erreicht, beginnt sich das Material im Querschnitt zu verjüngen. Das Einschnüren und der damit verbundene Verlust in der Materialdicke führt zu einer weiteren, schnellen und fortschreitenden Schwächung des Materials, bis der Metallstab letzten Endes zerreißt.

Die elastische Verformung (A)

In der ersten Phase des Spannungs-Dehnungs-Diagramms ist die Sprache von der elastischen Verformung. Sobald die, auf das Material einwirkende Spannung wieder gelöst wird, wird sich das Material wieder in die ursprüngliche Länge verkürzen. Dies wird als vollständige Rückverformung bezeichnet. Der Bereich der elastischen Verformung kann wiederum in zwei Phasen untergliedert werden. Die erste Phase dehnt sich das Material proportional zur einwirkenden Spannung aus. Diese Dehnung wird auch als linear-elastische oder proportionale Verformung genannt.

Dieses Verhalten von Werkstoffen im Bereich der proportionalen Verformung wurde bereits 1768 vom englischen Universalgelehrten Robert Hooke, im nach ihm benannten Hookschen Gesetz, beschreiben. Ist das Maximum der linear-elastischen Dehnung erreicht, spricht man von der Proportionalitätsgrenze. Jenseits dieser Grenze findet zwar immer noch die elastische Verformung statt, jedoch findet in diesem Abschnitt, unter der steigenden Krafteinwirkung eine stärkere Dehnung statt. Die Dehnung ist also größer als die zunehmende Spannung.

Die Fließzone (B)

Eine weitere, geringe Zunahme der Spannung kann schon zur Überschreitung der Proportionalitätsgrenze führen. Unter dieser Krafteinwirkung beginnt das Material zu fließen und es kommt zu ersten plastischen Verformungen. Der Bereich, in dem das Material fließt, liegt zwischen der unteren und oberen Fließgrenze. Der höchste Fließpunkt wird als erstes erreicht, welcher mit einem ersten, plötzlichen Qualitätsverlust einhergeht. Dadurch nimmt die benötigte Spannung, das Material weiter zu dehnen, sofort ab und erreicht den niedrigsten Fließpunkt.

Nach dem Überschreiten dieser Punkte hat sich das Material definitiv irreparabel verformt, selbst wenn die Krafteinwirkung sofort gestoppt werden würde. Bei weiter steigender Kraftweinwirkung, beginnen die im Material vorhandenen Kristallfehler (Versetzungen) zu wandern und sich zu vermehren, was wie beim ersten Fließpunkt zu weiteren Qualitätsabfällen führt und sich Spannung und Dehnung unregelmäßig zueinander verhalten. Dadurch entsteht der charakteristische, wellenförmige Kurvenverlauf.

Die Materialverfestigung (C)

Wird die Spannung weiter auf das Material erhöht, bilden sich zunehmend stehende Versetzungen im Kristallgitter, die die vorher noch gleitenden Versetzungen in ihrer Bewegung behindern. Dabei nimmt die Spannung im Kristallgefüge weiter zu, was zu einer Verfestigung des Materials führt. Das führt dazu, dass für eine weitere plastische Verformung eine immer größer werdende Kraft benötigt wird. Dieser Prozess ist jedoch nicht unendlich fortführbar. Jedes Material hat sein spezifisches Kraftmaximum.

Die Einschnürung (D)

Wird das Kraftmaximum überschritten, beginnt sich das Material einzuschnüren. Im Kristallgitter des Metallstabes haben sich dann so viele Versetzungen gebildet, dass die nicht mehr zu einer Verfestigung führen sondern zur Bildung von Hohlräumen beitragen. Neben den Einschnüren führen auch die Hohlräume zu einer Verminderung des Materialquerschnittes. Die Spannung wirkt nun auf einen immer kleiner werdenden Querschnitt, wodurch sich dieser Prozess zunehmend verstärkt.

Im weiteren Verlauf des Zugversuches verstärkt sich die Einschnürung so stark, bis der verjüngte Querschnitt die Spannung nicht mehr halten kann. In diesem Augenblick reißt der Metallstab an der schwächsten Stelle.

Das Spannungs-Dehnungs-Diagramm handhaben

Das Diagramm zeigt, wie sich Materialien unter zunehmender Krafteinwirkung verhalten. In der Praxis ist die Fließgrenze ein Wert, da sich ab diesem Punkt Materialien plastisch verformen. Bei Rime ist dieser Wert von großem Interesse, da sich ab diesem Punkt Blechtafeln durch Abkanten oder Rundbiegen umformen lassen. Besonders bei tragenden Konstruktionen muss stets darauf geachtet werden, dass die Belastung niemals die Fließgrenze erreicht, damit sich diese nicht unerwünscht verformen.

Aus dem Diagramm können einige wichtige und aussagekräftige Kennwerte abgelesen werden

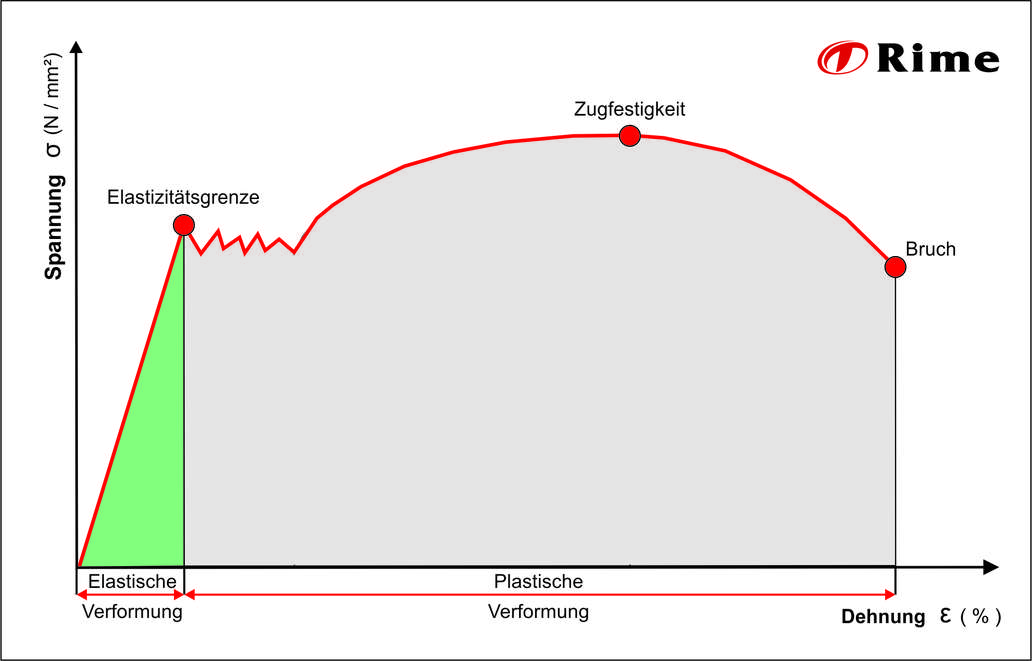
Elastizitätsgrenze

Am Anfang eines Zugversuches verhalten sich Spannung und Dehnung proportional zueinander. Im Diagramm ist dies durch den geraden Verlauf des Graphen zu erkennen.

Der Endpunkt des geraden Verlaufs ist die Proportionalitätsgrenze, die bei vielen Metallen auch der Elastizitätsgrenze entspricht. Eine Rückverformung in den Ursprungszustand ist nur möglich, wenn dieser Punkt nicht überschritten wurde.

Zugfestigkeit

Dieser Wert gibt darüber Auskunft, wie stark ein Werkstoff maximal belastet werden kann, ohne dass sich eine Einschnürung bildet.

Bruch

Dieser Wert gibt an, ab welcher Belastung die Einschnürung des Materials so stark ist, dass der verjüngte Querschnitt der einwirkenden Spannung nicht mehr standhalten kann und an der schwächsten Stelle bricht.

Variablen im Spannungs-Dehnungs-Diagramm

steif / elastisch
Im Bereich der elastischen Verformung verläuft der Graph in einer geraden Line. Vom Steigungswinkel dieser Gerade kann man ableiten, wie steif das Material ist. Umso steiler diese Line ansteigt, desto steifer ist der Werkstoff. Verläuft der Graph flacher, handelt es sich somit um ein elastischeres Material.
hart / weich
Desto höher die Grenze liegt, in der das Material zu fließen beginnt, desto härter ist es. Härtere Materialien haben den Vorteil, dass sie viel mehr Kräfte aufnehmen können bevor sie sich verformen. Dies ist besonders für tragende Konstruktionen wichtig. Weiche Werkstoffe lassen sich dafür einfacher Verformen.
stark / schwach
Starke Werkstoffe können viel höheren Spannungskräften standhalten. Schwache Werkstoffe bilden schon bei geringerer Spannung schnell Einschnürungen aus, wodurch sie auch eher reißen.
spröde / zäh
Die letzte wichtige Eigenschaft ist die Unterscheidung in spröde oder zähe Werkstoffe. Spröde Materialien vertragen wenig Zugkraft und brechen deutlich schneller. Zähe Werkstoffe haben außerdem den Vorteil, dass sie bei Überlastung starke Verformungen ausbilden bevor sie reißen. So werden Materialermüdungen schon lange vor dem Zerreißen visuell sichtbar, sodass darauf noch reagiert werden kann.